The current chapter on expected value and combining distributions in AP Statistics is one of my favorites for a number of reasons. First, we have the opportunity to play games and analyze them…if you can’t make this fun, you are doing something wrong. Second, it often feels like the first time in the course we are doing some heavy lifting. Until now, we have discussed ideas like sampling, scatterplots and describing distributions – nothing really “new”, though we are certainly taking a much deeper dive.
The section on combining distributions contains a number of “major league” ideas; non-negotiable concepts which help build the engine for hypothesis testing later. The activity I’m sharing today will focus on these facts:
- The variance of the sum of independent, random variables is the sum of their variances.
- The variance of the difference of independent, random variables is the sum of their variances.
- The sum of normal variables is also normal.
First, we need to have student “buy in” that variances add. Then we have the strange second fact: how can it be that we ADD variances, when we are subtracting random variables? In this activity, we’ll look at large samples, and what happens when we add and subtract these samples. Since many students taking AP Stats have the SAT on their brain, and there is a natural need to add and subtract these variables, we have a meaningful context for exploration.
SIMULATING SAT MATH AND VERBAL SCORES
The printable classroom instructions for this activity are given at the bottom of this post.
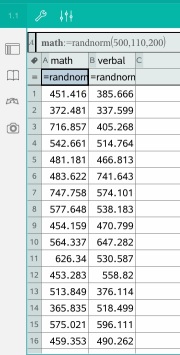To begin, students use their graphing calculator to generate 200 simulated SAT math scores, using the “randnorm” feature on their TI calculators, and using the fact that section scores have an approximately normal distribution with mean 500 and standard deviation 110. Note – some older, non-silver edition TI-84’s won’t be happy with this, and a few students had to downgrade and use a sample of size 50 instead. There are a few issues with realism here: SAT section scores are always multiples of 10, which randnorm doesn’t “know”, and occasionally we will get a score below 200 or above 800, which are outside the possible range of scores. Also, there is a clear dependence on SAT section scores (higher math scores are associated with higher verbal scores, and vice versa), and here we are treating them independently. But since our intent is to observe behavior of distributions, and not reach conclusions about actual SAT scores, we can live with this. In my class, no student questioned this as problematic.
Repeat the simulation in another column to simulate verbal scores. Then, for both columns, compute and record the sample mean and standard deviation. For my simulated data, we have the following:
It’s time to pause and make sure all students are clear on what we are simulating. We now have 200 students with paired data – the math and verbal score for each. Like most students, our simulated students would like to know their overall score, so adding math and verbal scores is natural. I help students write this command in a new column, then let them loose with the remaining instructions on both sides of the paper.
Students had little trouble finding the sum of the math and verbal scores, and computing the summary statistics. For my sample data, we have:
As students work through this, I want to make sure they are making connections to the notes they have already taken on combining distributions. I visited each student group (my students sit in groups of 4) to discuss their findings. Most groups could quickly identify that the means add, but what about those standard deviations? By now, if my students have taken good notes, they know that standard deviations don’t add, and that variances should. I leave groups with the task of verifying that the variances add.
Here’s the beautiful thing: students who immediately tell me that they “checked” the variances and verified the addition get the evil eye from me. In this simuation, students should find that the variances are “close” to adding, but not quite. At the end of the acitivity, I ask students to conjecture why the addition is a “not quite” – even after I have beat into them that variances add. There are two main reasons for this, and I was happy that a number of students sniffed these out.
- We are dealing with samples, not populations. There is inherent variability in the samples which causes the sample variances to not behave nicely.
- Variances add – but only if distributions are independent. Here, even though we created large random samples, there is still some small dependence. And while we don’t specifically cover the formula for dependent distributions in AP Stats, it’s worth discussing.
Next, it’s time to look at the differences. Here’s students are asked to subtract math and verbal scores, compute the summary statistics, and compare the sum and differences. This was a nice way to go back and re-visit center, shape and spread.
CENTER: Sums are centered around 1000, while differences are centered around zero.
SHAPE: Both distributions appear approximately normal.
SPREAD: The sum and difference distributions appear to have similar variability.
And this idea that the spread, and standard deviation, will be similar for both the sum and difference, can be also be explained by looking at the range of each population distribution.
- For the sums, the max score is 1600 (800 M and 800 V), with a min of 400 (200 each)
- For the differences, the max score is +600 (800M and 200 V), with a min of -600 (200M and 800 V).
Here, we can see that both distributiuons has the same range.
From start to finish, this exploration took about 30-40 minutes, and was worthwhile for verifying and developing understanding of the facts for combining distributions. The student instructions and video notes students take beforehand are given below. Enjoy!
This past week I caught up on past episodes on the Freakonomics Podcast while working out. One episode from November was of particular interest, titled “
mathcoachblog 