Category: Algebra

Today is student choice day, where I look through the Edmodo submissions from my students and choose a short and snappy opener.  Chris B. submits this number “magic” as a video worth sharing with the class:

What’s going on here? Is it just plain coincidence? Dumb luck? The devil’s work? 37 is certainly not a number we encounter too often in our daily math life.

A student in my afternoon class quickly picked up on the mystery:

37 times 3 is 111, and they all have 111 in them

Good enough. Converting a division example from the video into multiplication helps verify the claim”

777 = 37 * 21
111 * 7 = 37 * 3 * 7

It’s a quiz day, but I leave the class with the following challenge:

Develop a similar pattern for a longer string of identical numbers

They are pretty easy to find, such as the one below for five-digit strings. And Chris provided a low-stress math challenge to get us into math thinking mode before our quiz.

We’re moving through our algebra review, and today is absolute value day! I’m not sure the students are as thrilled about this as I am –

My students have seen absolute value equations and inequalities before, mostly as a stand-alone unit with a series of special rules to memorize. But I find that students have rarely been asked to think about solutions to inequalities as the comparison of values between two functions. So instead of re-hashing some old rules, let’s fire up the netbooks and look at some graphs!

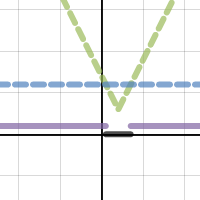The Desmos desmonstration here (it’s clickable) allows students to experiment with the parameters of an absolute value function, and compare to a constant function.  Before diving into some specific problems, I allowed a few minutes for partnerships to play and try to summarize any relationships they saw.  Very few saw an immediate link to what we have already been working on – inequalities – and the best was yet to come.

To start thinking about specific inequalitiy problems, I asked students to set the sliders so that they represent the following problem:

The graph then lets us analyze the relationship between the absolute value function (dashed green) and the constant function (dashed blue).

Time to find out if my students see the link between the graphs and the inequality. Groups were given 2 minutes of “table talk” to discuss:

How does this graph allow us to find solutions to the given inequality?

This was not a quick discussion. Many students were eager to participate and provide ideas, but many went back to pencil and paper, rather than analyze the graph.  Soon, with some students approaching the board, links beween the green and blue functions were found.  But, if scaffolding is needed, think about these prompts:

• When is the green “above” the blue? What does this indicate?
• When is the green “below” the blue? What does this indicate?
• Where do the green and blue intersect?

Finally, students began to understand the meaning of the black and purple lines on the graph – representations of the “greater than” and “less than” solutions sets.

In the end, I find that using technology to analyze the visual relationships between functions allows for a deeper understanding than algebraic maniupulation alone. Yet, I am often surprised when students don’t know that this is a valid (not “cheating” or somehow dirty) method of solving an equation. To assess what parts of this lesson “stuck”, I plan to give the following opener tomorrow.  Solve for x:

Wondering how many will immediately whip out Desmos on their cell phone….hoping they do!

After a first half of the semester filled with Probability and Statistics goodness, my freshman course now shifts to algebra topics, and a bridge between topics many have not seen for 2 years as many of these students took algebra 1 in 7th grade.  The next few days will be a blitz of past ideas: slope, linear functions, inequalities and absolute value.  Today, one of my favorite pictures from Dan Meyer‘s fun site, 101qs, is quite a conversation starter:

Why did they built it like that? How do they eat in that house?  How do they get in the front door?  What’s the bathtub like?  All are questions generated by the class.  You can enjoy more interesting questions generated by guests to the 101qs site. And we are off are running with slope!

I find that my students coming to the HS from our middle school have been trained well in navigating slope-intercept form for linear equations.  There are some stumbling blocks with fractions, and I need to do some hand slapping to keep kids away from their calculators, but I am mostly satisfied with where students are with slope-intercept form.

Standard form, meanwhile, is quite a different story.  Asking students to convert from slope-intercept form leads to painful moments: moving terms, and multiplying to rid ourselves of fractions.  But it also allows for entry to a new idea – leveraging relatioships with standard form and developing a new formula for slope, m = – A/B.  Developing this via some examples, and letting a few crackerjack students summarize this finding for the class, opens the door for a new method for finding the equation of a line.  Now, when presented with a slope and a point, we have two options.

OPTION 1: find the equation in slope-intercept form and convert to standard form. Messy, and some nasty fractions can appear!

OPTION2: use what we have now discovered about slope and standard form to build our equation directly in standard form, and solving for C.

“Why didn’t they just show us this in middle school?!!!”  Well, maybe you weren’t quite ready then, or maybe standard form isn’t the star of the show it needs to be. In any case, today was a great day to combine old skills with some new explorations and keep things feeling “fresh”.  Tomorrow, the payoff will continue when we look at parallel and perpendicular lines, as homework tonight expands on today’s theme.