Tag: algebra

Categories
Class Openers

Class Opener – Day 16 – A Revealing Discussion of Factorial

I opened today with what I had hoped would be a rich discussion concerning a past contest problem, but turned into something more substantial.  Here is the problem:

2014-09-23_0002

I wasn’t too surprised when many, many students reached for their graphing calculator…this is what freshmen do. I was however surprised when I asked the class to volunteer their ideas on how they could simplify the expression – placing ideas on the board.  Some appear below, and we discussed why or why not the procedures were valid.

photo1 photo2

Many misconceptions regarding what it means to “cancel” in a fraction were revealed; in fact, the very nature of what it means to reduce was the star of our discussion.

2014-09-23_0003Later in class, I provided a hint which I hoped would provide some clarity with our factorial challenge. Some students immediately saw the link to the original problem and simplified. But how much closer are wo to finding the largest prime divisor? After simplifying, it was back to the calculators….which doesn’t really help much here.  Listing the remaining factors of 16! after dividing common factors of 8! leaves us with the clear answer : 13.

The moral of the story – those who never touch a calculator discover the mechanics of this problem much more quickly than those who take a sledgehammer to it with a Nspire CX.

Categories
Algebra

Hitting the Home Stretch: Exponents, GCF’s and LCM’s

This is a busy stretch in my school year.  My 2 Prob/Stat classes are nearing the end of new material with PA Keystone Exams in Algebra 1 looming. For my College Prep class, about half have not yet taken the Keystone while the rest took it last year as 8th graders. In Academic, all students will take the Keystone in May.  Combine this with my AP Stats class taking their final exam this week, with the AP Exam next week, and my track and field meet responsibilities building as the season reaches its peak; it’s a hectic time of year.

In both of my Prob/Stat classes, we are beginning unit on polynomials.  The Prob/Stat class is a course we offer between Algebra 1 and 2. While the course contains much Prob/Stat material, we also clean up some concepts from algebra.  Unlike other algebraic units like systems of equations where there are many rich examples and opportunities to differentiate, the start of a polynomials unit often feels static. Here are two activities I have used this week for Laws of Exponents and GCFs/LCM’s.

LAWS OF EXPONENTS – TRUE/FALSE GROUPS

This activity worked equally well in my college-prep group (for whom this was review material), and my academic group (where this was mostly new).  The file below contains 16 cards with numeric statements.  Break your class into teams of 2, 3 or 4.  The job of the group is to identify the true statements and the false statements.  For this activity I banned all calculators.

View this document on Scribd

The letters on the cards are not anything the kids need to worry about, but allow me to easily check progress. The cards with vowels are all the false statements.

I was surprised at how much trouble my college-prep group had with building the correct false pile.  To reach some consensus on the false pile, I asked every group to hold up one card they knew to be absolutely, positively false.  Many groups mistakenly agreed that any number raised to the zero power was worth zero, which led to a class argument on who was right.

Tomorrow, we will look more closely at the falses.  In the file above, note that the cards are arranged in groups of 4. In the first group, we will review the addition rules for exponents; then the subtraction rule in the next group of 4; then the multiplication rule for the next group.  In the end, this felt much more satisfying, with increased engagement and peer discussion than simply listing rules on the board.

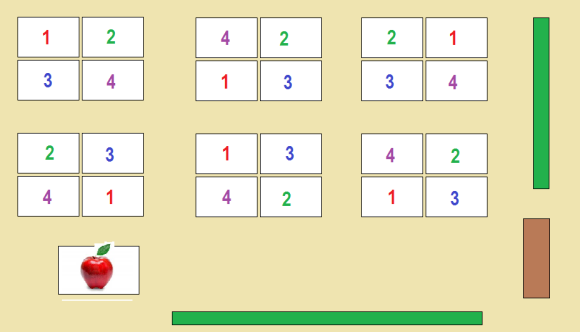
GCFs and LCMs SPEED DATING

The speed dating concept is one many math teachers have stolen from the great Kate Nowack, and it worked perfectly in my Academic class to work through greatest common factors and least common multiples.  After doing just one example on the board, desks were arranged  into a pairs facing each other, down one long row.

Speed Dating

All students were given a card with a monomial.  They then worked with their partner facing them, and found the GCF of the two monomials.  The first time around, my co-teacher and I provided help to just about all groups.  After teams found their GCF’s, all students on the right-hand side stood and moved down one seat and worked with their new partner.  There were so many plusses to this activity:

  • all students were repsonsible for their own monomial
  • all students were engaged: no hiding behind a worksheet
  • students worked together, and with different partners each time

Some of the cards I handed out are shown here.  I tried to have a variety of cards which clearly shared factors, with different powers of x and y.

cards

I was very impressed with how my class performed on this activity, and we moved onto a second round where LCM’s were found. This time I had students trade cards, and the left-hand side shifted down each time.

Let your kids work together, discuss and find patterns – the notes then write themselves.

Categories
Algebra

The Binomial Theorem Jigsaw

Is there a rule in math which encapsulates more great stuff than the binomial theorem?  Increasing powers of x, decreasing powers of y, a bunch of terms to look at…and hey, what’s this….combinations, you say?  I’m in.  But please don’t remove all the fun discovery moments there are to be had here.  Here’s a jigsaw activity which was handed down by some of my “senior” and now-retired colleagues, and is now infused with my need to get kids moving around and discovering things.  I hope you enjoy it.

The students will need some background on a few things here.  In particular, students should already be fluent with multiplying binomials, and have some familiarity with combinations.  Copy the first 4 pages of the binomial theorem Jigsaw Activity and have them ready to go.  Now it’s time for some movement.

Arrange classroom desks into groups of 4.  If your class roster number is not a multiple of 4, then you can have some 5’s, and we will deal with them soon.

binomial

In each group, have the students number themselves from 1 to 4.  It is important that each group have one of each number, and that students know their number. If you have any groups of 5, then allow for two “1’s” in a group.  This will be helpful, as #1’s actually have the trickiest job in this task (but don’t tell them that yet!).

binomial1

Next, hand out the packet of tasks.  The packet looks intimidating, but each student is only responsible for completing one page.  All students who are “1’s” are responsible for completing Task 1.  2’s will complete Task 2.  3’s = Task 3.  And 4’s have Task 4.  On your command, students will break from the group, and move to a new location and meet with all oftheir  similarly-numbered classmates to complete the task together.  After all students have completed their task, they will re-join their group and share their findings.  It is important that students understand the need to complete their task thoroughly and thoughtfully, as their group success depends upon it!

binomial2

Now, send all the numbered students to meet with their group and complete their task:

SUMMARY OF THE TASKS:

  • In Task 1, students are asked to expand (x+y)^4, starting with (x+y)^2 and working their way up.  This task usually takes the longest for groups to complete, and requires attention to detail.  In the end, groups are asked to list the co-efficients of the terms they get.
  • In Task 2, students are asked to list the sample space for 4 tossed coins.  The task is not difficult, but requires attention to detail in making sure all possibilities are provided.  Groups are then asked to list number of ways to get 0 heads, 1 head, 2 heads, etc., in the 4 coins.  Note, groups often give probabilities here….we want the COUNTS!
  • In Task 3, students complete a number of rows in Pascal’s Triangle.  The task in not tricky, but requires attention to detail in filling out the small boxes.  The group is then asked to list the numbers in row 4 of the triangle.
  • In Task 4, students are asked to compute a number of combinations by formula.  I usually try to have 4-function calculators at the ready for this group, and want them to really focus on the formulas.  In the end, the group is asked to list the combinations of 4 items taken 0, 1, 2 3 and 4 at a time.

The tasks often take about 20-30 minutes for groups to complete and check.  Bringing groups back together and having them share their findings with their teammmates often takes another 20-30 minutes, so this may need to be done over 2 days.

binomial3The big reveal occurs as groups begin to realize that all 4 tasks have the same “answers”:

1-4-6-4-1

We’re now ready to start exploring the amazing connections between 4 ideas (binomials, coins, Pascal’s Triangle, combinations) which seemed quite different math-wise, but have some strong connections.  Now the ideas come fast and furious as we explore the connections.  Page 5 of the packet provides some guiding questions, but don’t feel tied to the linearity of my questions.

Let’s think about (x+y)^5…..

  • How many terms will it have? 6
  • How will the powers of x and y behave?
  • How can we find the coefficients?  Pascal’s Traingle!
  • How else can we find the coefficients?  Combinations!

How about coin flipping:

  • If we flipped 6 coins, how many items would be in the sample space?  2^6
  • How many of these possibilities will have all heads?  1
  • How can we find out the number of ways to get exactly 2 heads?  Pascal’s Triangle

Eventually, this will become the basis for “assembling” the Binomial Theorem.  You’ll be surprised at how much of it your students will be able to piece together after this activity.  Your job is to just help out with some symbols and some common language.