Last spring, the awesome folks at Desmos released a slew of slick (but easy-to-use) statistics features. Here is a brief video I made which walks through a few of the new features. With a new academic year beginning, I’m looking forward to changing some of my classroom moves in AP Stats to leverage the new features and build understanding. Here are 3 moves I’m planning to try this year:
ASSESSING NORMALITY (Here is a previous post on this topic)
Pop quiz! Below you see 6 boxplots. Each boxplot represents a random sample of size 20, each drawn from a large population. Which of the underlying populations have an approximately normal shape? Take a moment to think how you…and your students…might answer…

Have your answers ready? Here comes the reveal…..


Not only do each of the samples above come from normal populations, they each come from the same theoretical population! This year in class I plan to walk students through how to build their own random sampler on Desmos, which takes only a few intuitive commands. When the “random” command is used, we now get a re-randomize” button which allows students to cycle through many random samples and assess the shapes. You can toy with my graph here.
Often students look for strict symmetry or place too much stock in different-sized tails. This is a great opportunity to have students explore and understand the variability in sampling. Teach your students to widen their nets when trying to assess normality and remember – our job is usually not to “prove” normality; instead, these samples show that the assumption of population normality is often safe and reasonable, especially with small samples.
LINEAR TRANSFORMATIONS OF DATA

Analyzing univariate data using Desmos is now quite easy. Let your students build and explore their own data sets. Data can be either typed in as a list or imported from a spreadsheet using copy/paste. The command “Stats” provides the 5-number summary, and commands for mean and standard deviation are also available. You can play around with my dataset here.
Next, I want my students to consider transformations to the data set. In my example I have provided a list of test scores and summary statistics are provided. Let’s think about a “what if”. In the next lines I provide 2 boxplot commands, but I have intentionally ruined the command by placing an apostrophe before the command (thanks Christopher Danielson for this powerful move!). What will happen if every student is given 5 “bonus” points? What if I feel generous and add 10% to everyone’s grade?

What will happen when I remove those apostrophes? Think about the center, shape and spread of the resulting boxplots? How will these new boxplots be similar to and different from the original?
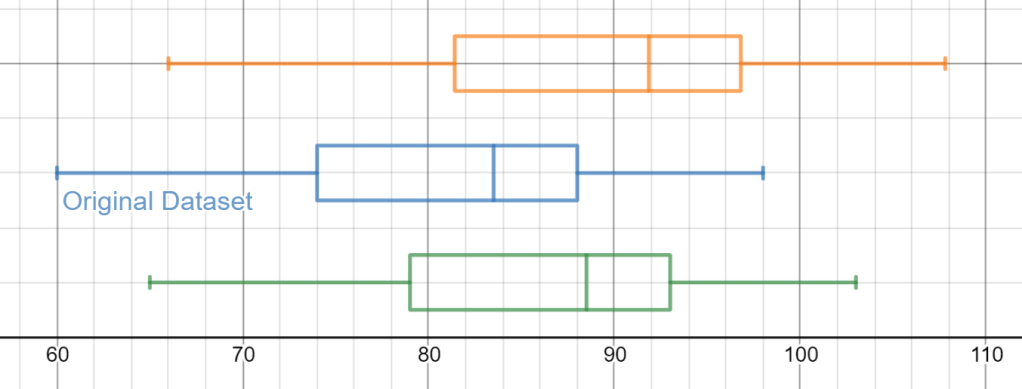
Compute new summary statistics. Which stats change…by now much…and what stays the same? Why? I’m looking forward to having students build their own linear transformation graphs, investigating and summarizing their findings! Here is a graph you can use with your classes to explore these linear transformations with sliders.
COMBINATIONS OF DISTRIBUTIONS
An important topic later in AP Stats – what happens when we combine distributions by adding or subtracting? Often I will use SAT scores as a context to introduce this topic because there are two sections (verbal and math) and a built-in need to add them – What are the total scores? On which section do students tend to do “better”…and by how much? To build a Desmos interactive here, I start with a theoretical normal distribution with mean 500 and standard deviation 100 to represent both mean and verbal score distributions. Next, taking 2 random samples of size 1000 and building commands to add and subtract them allows us to look at distributions of sums and differences and compare their center, shape and spread.


The most important take-away for students here should be that distributions of sums and differences have similar variability. This is a tricky, yet vital, idea for students as they begin to think about hypothesis tests for 2 samples. You can use my graph, or build your own. Note – in my graph the slider is used to generate repeated random samples.