Category: Uncategorized

If you are a loyal followed of the blog (and I know you are!), you’ll notice there was no class opener this past Friday.  This is because I was not in school, and instead traveled about an hour north of my home to New Brunswick, NJ. for the Association of Math Teachers of New Jersey annual conference. I facilitated a fun hour of tech tools for math class (Padlet, Poll Everywhere, Answer Garden, etc…) and couldn’t help myself but to unveil Desmos regressions to an appreciative group of Desmos lovers.

But the highlight of the day was my participation in an Ignite session, hosted by my friends at the Drexel Math Forum. 10 speakers each had 5 minutes to get their ideas across through 20 slides which changed every 15 seconds. It’s a fun an intimidating concept!  Some of those who shared during the Ignite were Max and Annie from the Math Forum, Phil Daro, past NCTM President Jim Rubillo….and me?  How the hell did I get invited to present with a group of people I admire so much?  I think my topic, language in math class (based on a past blog post on math phrases I’d like to see expunged) went over well, and I look forward to sharing the video when it becomes available.  It’s probably the most thrilling experience I’ve had as a speaker.

---

But the fun math times continued after the Ignite session, when Jim Rubillo and I shared a conversation about the exciting role of technology in math class, and its ability to allow students to investigate ideas efficiently.  It turns out that Jim lives about 10 minutes from me (small world) and he shared a math idea from his (I think) college math course where students used technology to pursue an idea.

This particular investigation involves the Harmonic Series, which I have shared with my freshmen classes recently:

This series diverges, heading off towards infinity – though quite slowly, and Jim’s students investigated when the series passed integer values. How many terms does it take for the series to go above 3, or 4, or 5, etc?  Some examples:

• When n=4, the sum climbs above 2
• When n=11, the sum climbs above 3
• When n=83, the sum climbs above 4
• When n=227, the sum climbs above 5

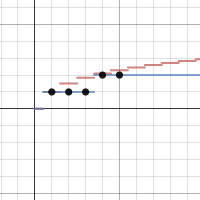Technology was uber-useful here, as a Desmos graph (click the picture to the right to explore) allowed me to observe the sum, and use a Floor function to watch when the next integer value is reached.  A table was also useful to verify the changes in sum.

This was all done after I went home that day, and it was Jim’s next challenge when had me intrigued:

If you look at the n’s where the sum reaches a new integer value, and find the ratio of these consecutive n’s, you’ll never guess what the ratio approaches.

Well, in math, there are lots of surprising results, and many of them seem to involve a few “usual suspects”.  I really had no idea what those number might approach – but I had a good guess: “I bet it’s e”.

Yes! It’s e!!! Shared Jim excitedly, with a pretty good punch to the arm.

Some quick calculations involving these landmark n’s seem to lend some evidence towards Jim’s claim.  It’s an idea he said he had never seen before, and I don’t recall encountering it.  But Jim did find some documentation regarding a proof, but couldn’t recall where it was located.  If anyone out there has more info to share, please contribute in the comments!

In the end, Friday was just an awesome day of sharing, and fun to talk one-on-one with some legends in the math education community.

“Math needs better marketing” – Neil deGrasse Tyson

---

Today is the last day of summer. Tomorrow, a week of district PD begins in my district, followed by the first day of school just after labor day. It’s a great time to reflect upon a summer of learning and how I will use what I have learned to improve my instructional practice.  Upon reflection, I have reached one scary conclusion.

I am the problem with math education.

It’s true.

It’s not that I am a bad teacher (I hope not anyway….).  My students do well, I work to improve myself professionally, and I try my best to share what I know with colleagues.  But what happens inside the classroom walls just isn’t enough anymore.

Recently, I was driving with my sister, and the conversation turned towards school and how my niece and nephew were doing.  The topic of math was certain to come up, in particular how math “looks” differently now in some ways than how we were taught.  It was then that my sister summarized her observations of today’s math homework:

“It’s retard math”

I could have responded with an explanation of what I knew about the common core. About the need to have students experience math differently, through partial products, through thinking in groups, by drawing arrays, and the certain value all of these alternative approaches would hold in building understanding as her children head towards Algebra, where thinking abstractly now will be a huge benefit. I could have given her a synopsis of my thoughts on the off-base and overly-simpistic Facebook posts regarding standard algorithms vs “new” methods, or how the Standards of Mathematical Practice are changing how math teachers consider instruction.   I could have told her how Frank Noschese and Chris Robinson are super-heroes, for standing up to all of us in their twitter discussions with sound-bite artists.

But I didn’t do any of that.

I let the subject drop.

It was just easier that way.

Rather than entertaining a real debate, I gave up. And that’s a problem.

This clip featuring Neil deGrasse Tyson summarizes why we need math, and why we need to promote the pursuit of higher-level math now more than ever.

At this year’s Siemens STEM Institute, Cindy Moss challenged us all to think about what we would do in the next 6 hours, 6 days, 6 weeks, and 6 months relative to what we had learned at the Institute.  I never did make that list. So with one last night before the start of another school year…here goes:

• 6 hours: write this post and share out Cindy’s great thoughts and ideas by sharing the Livestream below.
• 6 days: share some great new tools, and work with my colleagues to develop effective practices around them
• 6 weeks: start a new part of the blog of my daily math class openers. I use many videos, resources, and stories to open my class, even if they are not connected with the current content. These are often the highlights of our learning day.
• 6 months: have a serious conversation with my sister about why drawing arrays or counting rainbows isn’t “retarded”.

This year’s school resolution – be more aggressive in highlighting new and innovative practices, and work to be a more effective instructional leader.

If you have an hour, enjoy Cindy’s talk below. You’ll pick up some great ideas, and feel energized about your ability to make STEM work at your school.

http://new.livestream.com/DEN/events/3216756/videos/58528261

There’s so much goodness from Twitter Math Camp to share, and only so many blog posts! Today I want to share two great ideas for assessing student understanding during a unit.

HINGE QUESTIONS

In an afternoon session, my friend Nik Doran led a session on hinge questions: questions diagnostic in nature, not only intended to assess students understanding, but also carefully written to categorize students by their cognitive misconceptions. Many of Nik’s examples were multiple-choice, and I appreciated the subtle differences between the responses which predict student errors. In addition, I liked Nik’s suggestions for how to work with students after these questions: by grouping them by error, differentiating instruction based on correctness, and/or having students defend their response choice.

On Nik’s blog, you will find a wealth of resources regarding these questions, including blog posts on hinge questions and formative assessment research from Dylan Wiliam.

Breaking into content-based teams, the group then attempted to build their own hinge questions. Here are my observations regarding the crafting of these formative experiences:

• Keep it simple. One team attempted to build a question around solving a quadratic equation. The question required terms to be moved, then irrational solutions found. There were too many places where students could trip up that it was impossible to pigeon-hole student responses into neat boxes.
• The issue of non-response came up in discussion: how to tell the difference between a student misconception, and a guess. To me, this factor is minimized by limiting hinge questions to “big ideas”. We shouldn’t ask hinge questions on topics which have limited entry points. Every student should have some basic understanding of the task at hand.
• Use hinge questions in lessons where you have observed patterns of errors, and can easily describe them.

In my example below, I chose to tackle binomial probability, where the set-up of an expression has a number of possible “land mines”.

In a large batch of metal parts, it is anticipated that 15% of the parts will contain a defect. If a random sample of 20 parts is taken, what is the probability that exactly 4 of the parts will show a defect?

My multiple-choice selections are given below:

In A, students will mis-interpret the number of successes and failures in the problem, though the combination is correctly done.

In D, the required combination is incorrect, while the rest of the expression is correct.

In E, the number of successes and failures as exponents have been reversed.

Note that both B and C are correct, and I would be interested in having these two groups try to sell each other on the correctness of their response.

Do these reponses provide a complete picture of ALL mistakes students will potentially make? Probably not, but there should be enough information given for all students to make a reasonable attempt at the problem

---

Nik’s session leads me to one of the cooler tech-related happenings of the week.  Before a “My Favorites” session, I was handed a piece of paper with a strange design on it, and told that I would be asked to participate later in the session. Wow! I was chosen! So cool! But what is this thing? It’s not quite a QR code, and it seems a number of other folks were given similar pieces of paper. I’m not special after all….

For this sharing session, the group was asked a multiple-choice question. Those of use with the figures were asked to hold them up high so that the letter of our response was on top (note the letters on each side of the figure). With 40 cards in the air, the presenter scanned the room with her cell phone and…..what!!!…our choices were recorded on screen! How cool! I admit I get pretty geeked out when I see a cool tool, but this was seriously impressive. And these are Plickers, and app you can load, with free response cards you can download. Definitely looking forward to trying out this tool for formative assessments.