Month: September 2013

Categories
Algebra

Visualizing Shared Work Problems

Fred can paint a room in 5 hours, working alone.  His friend, Joe, can paint the same room in 7 hours.  How long will it take for them to paint the room, working together?

It’s a shared-work party, people!  Get your party hats on and let’s look at a visual method for exploring these often mundane problems.  This past summer at Twitter Math Camp, I participated in an algebra 2 group where part of our time was spend considering methods to re-think the traditionl approach to rational functions and their applications.  Thanks to John Berray for the great conversations, which led to some changes in how I appoached shared work problems this year.

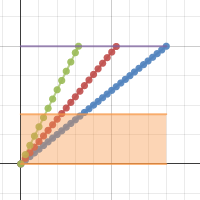
My approach this year started similarly to previous years: guiding a dicussion with the class, with the goal of developing models for the amount of work done by each painter.  I find that quesitons like “How much of the job will fred have complete after 1 hour? 2 hours…etc” will usually lead to the models we seek.  What I did differently this year was graph the two work functions.  Using the Desmos calculator works nicely, and allowed for a discussion of the problem much richer than if the expressions had been just jotted down on the board.  Many students followed along on their TI calculators.

SW1

From here, we can make connections betweem the functions, their graphs, and make conjectures about the sum of these functions.

SW2

In my class, students certainly completed similar problems (including distance / rate / time), with the graphs serving as a check and visual affirmation.  With the graphs, we could also look at adaptations to the theme, such as “what happens if one of the painters shows up 2 hours late?”

SW3

Also, problems where the combined time was given, with the goal of finding a missing individual rate, were explored and discussed.

SW4

Click the icon below to play with this model on your own.  This is a great opportunity to let students observe function behavior and communicate results from a graph.

UPDATE: The Desmos folks flew with this one, and added a whole bunch of bells and whistles.  Click the graph below to experience their shared-work extravaganza.

Categories
Statistics Technology

Rock, Paper, Scissors and 2-Way Tables

Last weekend, the evil Michael Fenton posted a link to an online applet which will now occupy you for the next 2 hours.  It’s not too late to run away now…

Still with me? An adventurous soul, you are.  Anyway, the NY Times online Science section has shared an online game of “Rock, Paper, Scissors”, where you can play against a choice of computer opponents.  The “Novice” opponent has no understanding of your previous moves or stratgey.  But, the “Veteran” option has gathered data on over 200,000 moves, and will try to use its database to crush your spirit.

RPS5

My Advanced Placement Statistics class today was preparing for their first chapter test, where topics include 2-way tables and marginal distributions.  Time to abandon my planned review and play!  Here’s what we did:

Each group (I have 6 groups of 4) was given a netbook computer and the NY Times site.  Half of the groups were told to play against the “Novice” player, while the other half challenged the “Veterarn”.  Each group played 20 times, and pride was on the line as groups considered their moves carefully.  Class data was gathered and compiled into a 2-way table.

RPS1

But just how good are we at outsmarting the computer opponent?  In round 2 of this activity, groups again played 20 games, switching their opponent.  This time, however, I directed groups to choose their moves RANDOMLY.  Groups used their graphing calculator to generate a random number from 1 to 3, which determined their move.  The NY Times site provides some info regarding randomization:

A truly random game of rock-paper-scissors would result in a statistical tie with each player winning, tying and losing one-third of the time. However, people are not truly random and thus can be studied and analyzed. While this computer won’t win all rounds, over time it can exploit a person’s tendencies and patterns to gain an advantage over its opponent.

Groups played 20 more times, and a new table was created for this “random” round.  Last round strategy was labeled the by “guts” round.

RPS2

With the data now on the board, groups were given a few minutes to summarize their findings.  Did we improve by being random?  Did we improve in any particular area?  This turned out to be an engaging review of marginal distributions, and a good opportunity to discuss ribbon graphs, which come up in AP Stats as a useful graphical display.  Below, Excel can be used to compare the “Veteran” opponent results.

Ribbon Graph

Thanks Mike, for sharing such a cool link!

Categories
Algebra Technology

I’ve Joined the Flipping Revolution

Two weeks into teaching Algebra 2 for the first time in a long time, and things are going great so far, but time to start one of the more potetnially tedius chapters in Algebra 2: Rational Expressions and Equations.  Taught “by the book” this can become a 2-week journey of nasty-looking expressions, scary worksheets and those dreaded “shared work” problems.  A perfect time for me to take my first real dive into “flipping” my classroom.  Here’s what I have done so far:

VIDEOS: I used Doceri to create videos for each of the sections in the chapter.  While I love Doceri (since I can do videos from my couch AND they upload easily to YouTube), using it for this chapter has not been ideal, since the problems get nasty and long quite quickly, and you can’t scroll the screen.  May use SMART Notebook for some down the road.  And a few “takes” were made, as it’s easy to screw up making a video when you have Jeopardy on mute in your living room.  Even my final version of the first video below has, for me, a “cringeworthy” error in vocabulary.  Here are my first two unit videos:

HOMEWORK:  Students have been given notesheets, with the problems in the videos provided.  Their job is to watch the video, take notes, and then complete just a handful of problems related to the idea.  My intent with these problems is not to provide anything tricky: just enough to demonstrate some mastery of the material.  We’ll save challenging problems for class.  All of this material is posted on Edmodo for my students, so they can go back if they need.

Just a few days in, and the reaction of the students has been quite positive.  They appreciate that they will not be given homework designed to keep them up for hours, and that the communication during class time is more whole-class, rather than lecture.  Some more classroom observations:

  • Homework is no longer an ending of a lesson, it’s the beginning of a journey.  Students come into class ready to apply what they experienced.  I have the ability to raise the difficulty of problems based on what I am sensing from the class.  I don’t need to wait until the day after a night of homework struggle to measure my students’ progress.
  • I am not spending a dis-proportionate amount of time at the beginning of class dealing with homework issues.  In earlier years, I assigned homework in the same manner I suspect many teachers do: give an assortment of problems..enough for students to feel successful, but with a few to provide challenge to those students who need it.  The next day, this approach often yielded well-intended, yet essentially wasteful, conversations where I went over problems in front of the class.  From my eyes, this seemed like “help” to the class, when from a wider view it is easy to see these discussions are only absorbed by small pockets of students.  And since the daily “let’s go over the tricky HW problems” portion of the day has been removed….
  • I am planning more investigative experiences into my routine.  Today, for the last 30 minutes of class, students borrowed netbooks from down the hall, and used Desmos to explore possible dimensions of rectangles with fixed area…a set-up for graphs of rational functions in a few days.  Part of this exploration turned into “play with Desmos, and do some stuff”.  Good!  Tomorrow, we will check out a shared-work video, and start making some connections.
  • Students are accountable for their learning.  They are welcome to view the videos multiple times, pause, or skip if they desire.  But, full disclosure….I am doing this now with an honors class.  Looking forward to trying his with my academic algebra 2 in the spring, and reporting out.
  • While I am using class time to tackle the most difficult problems, that is not to say my students to not have rigorous assignments.  Besides the “flipped” homework, I am also assigning more complex tasks, with a two-week window for students to choose, write-up, and turn in problems.  More on this in a later post.
  • I am also “flipping” lectures in AP Stats, through videos my colleague produced last year.  For these, I have created short Google Form quizzes which assess the main points of the video.  The data from these forms have been helpful in clearing up misconceptions during class meetings.
  • I will ALWAYS produce my own videos, or rely on those of my colleague for stats.  My students rely on me to be their guide, and I will always meet that expectation.  I will not let an anonymous guide be the primary source for my class.

Would appraicte your constructive feedback, suggestions, and classroom stories!  Now back to the iPad.