I’m a little off schedule with the class openers lately, so we’ll call this one day 55. There have been a few schedule disruptions here at school, and I was out yesterday – presenting on Standards Based Grading in Algebra 1 at the PASCD conference – on top of all of that, the dog ate my homework…..OK, enough excuses! Today really isn’t a class opener, but rather a summary of some goings-on related to math persistence – those times when you give your students a problem which will require more than a one-time effort, and observe their response.
 Jon Orr, a teacher from Ontario, shared the poster shown here on twitter, and I love it! If you aren’t following Jon, do it now, and be sure to check out his blog with lots of great classroom ideas, mostly for Algebra 1.
Jon Orr, a teacher from Ontario, shared the poster shown here on twitter, and I love it! If you aren’t following Jon, do it now, and be sure to check out his blog with lots of great classroom ideas, mostly for Algebra 1.
When I was out yesterday, my students had two tasks to complete: work through problems as review for their quiz on matrices today, and complete a “problem solving” task involving matrices. In the task, which you can download here, students are asked to find a matrix which is its own inverse, with a few restrictions.
One team today submitted a paper which did find what was requested, but left me uneasy:
The group clearly found a matrix which is its own inverse, but am I confident that they could generalize and perhaps find more? And are those “random numbers” they started off with actually random, or do they signify the end of a process which has not been communicated? I find that this is typical of a problem-solving process for many students – begin with some “random” numbers and hope that they lead towards a fruitful path. Hey, what’s the matter with good old “guess and check”, if the question at hand is answered? I don’t have a problem with this “brute force” method IF the process leads to a generalization, which this paper did not. I struggle with having my students move from “I got an answer” and towards “hey, now I see how this REALLY works”. All is not lost, however, as some students thought about variables and attempted to generalize, but then opted to plug and chug.
I’m looking forward to the group conversations we will have in the coming days surrounding this problem.
Tonight for homework I assigned a problem involving a wire being streched around the earth. Within 60 seconds the first all familiar call was heard: “I don’t know what to do!”. A sly smile from me and pointing out today’s quote sent the message that this cry wouldn’t get them off easy…it’s a hard-fought battle to get kids to move past theiur initial blockades and think.
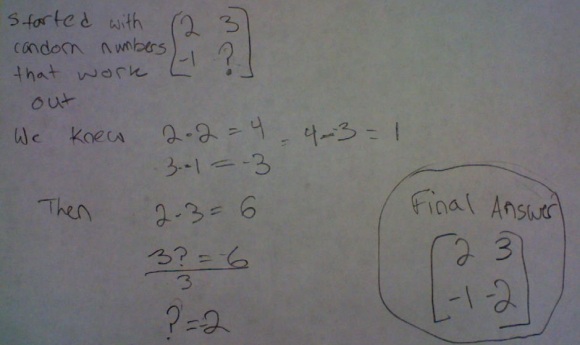
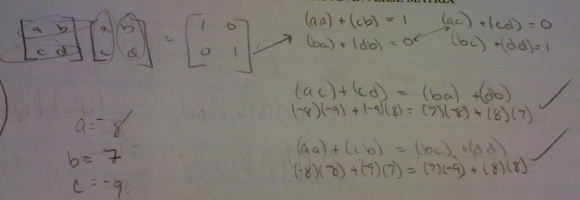
One reply on “Class Opener – Day 55(?) – Can We Just “Guess and Check”?”
Robert,
I love your class openers. Ever since I found your blog, I try not to miss these. I am not even a teacher by profession, but have an immense interest in teaching. I am the STEM teacher for my kids outside and beyond the classroom.
I think that most of us are conditioned to responding (narrowly) to what’s been asked. The kids might be more likely to do so given that they often have to complete the work within time bounds (on tests usually). That’s also the evil that leads them to memorizing algorithms without understanding the underlying concepts. Unless generalization has become an unwritten rule in your class, maybe the encouragement to generalize could come in the problem statement itself. For example, “short and sweet” would almost suggest not to generalize. Maybe, offer extra credit for figuring out a way to find additional answers quickly and without having to do the same thing all over again.
Shortcuts and pet algorithms are fine to use as long as we have figured them out or we can explain why they work.
Thanks,
Pawan