UPDATE – I recently posted more info about this project, with a rubric and more examples, at this post.
One of my favorite math projects takes place during our unit on conic sections in Algebra II. In the project, students are challenged to manipulate equations of conics and graph them using software to make pictures. I started with this project 12 years ago when a colleague, who has since retired, introduced me to his ideas. Back then, we used a DOS program which could only graph in black, cyan and magenta. We were happy if we saw a tree made from a hyperbola and a parabola leaf line.
The project grew new wings with a program called Math Toolkit, which allowed for finer graphing and the ability to save work. Later, we started using Print Screen to grab the graphs and move them into MS Paint. The projects grew more intricate, and many kids took off with their creativity.
This year, the Desmos online calculator brought the project to a new level. Students this year could work on their equations at home, save work, and work with their teacher during time allotted in class. Thanks to Kevin for working with his class to share their creations.
First up is Kristin. Her project moves from Desmos to Paint. Then un-needed pieces are removed, and the final product emerges.



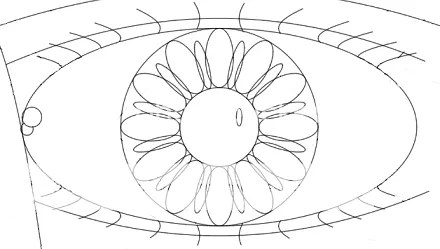
Next up is Matt. Here are his graphs after the axes and grid were removed….

Any ideas what the finished product will be?
Did you guess yet?
OK, so you just want to see it…ok….

What I love most about this project is when students discover how the conics behave, and experiment with them without fear. In the next example, Connor wanted to tilt his ellipses and researched on his own how to make that work using trig functions (did I mention that these kids haven’t had trig yet?).


In some years, I have had students peer-assess their work by creating an art gallery of their work. Giving each student 5 star stickers, I had students select their favorites. Contact me if you would like any of the instructions or rubrics I have used for this project in the past. Thanks again to Kevin and his Algebra II class!



