Is there a rule in math which encapsulates more great stuff than the binomial theorem? Increasing powers of x, decreasing powers of y, a bunch of terms to look at…and hey, what’s this….combinations, you say? I’m in. But please don’t remove all the fun discovery moments there are to be had here. Here’s a jigsaw activity which was handed down by some of my “senior” and now-retired colleagues, and is now infused with my need to get kids moving around and discovering things. I hope you enjoy it.
The students will need some background on a few things here. In particular, students should already be fluent with multiplying binomials, and have some familiarity with combinations. Copy the first 4 pages of the binomial theorem Jigsaw Activity and have them ready to go. Now it’s time for some movement.
Arrange classroom desks into groups of 4. If your class roster number is not a multiple of 4, then you can have some 5’s, and we will deal with them soon.

In each group, have the students number themselves from 1 to 4. It is important that each group have one of each number, and that students know their number. If you have any groups of 5, then allow for two “1’s” in a group. This will be helpful, as #1’s actually have the trickiest job in this task (but don’t tell them that yet!).
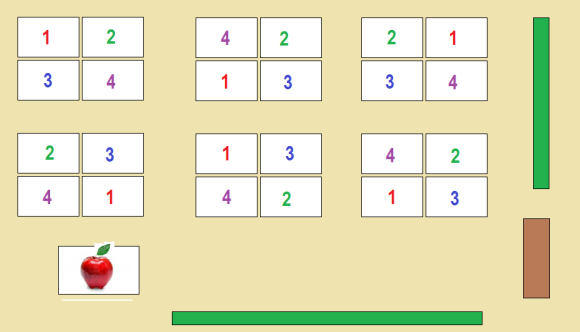
Next, hand out the packet of tasks. The packet looks intimidating, but each student is only responsible for completing one page. All students who are “1’s” are responsible for completing Task 1. 2’s will complete Task 2. 3’s = Task 3. And 4’s have Task 4. On your command, students will break from the group, and move to a new location and meet with all oftheir similarly-numbered classmates to complete the task together. After all students have completed their task, they will re-join their group and share their findings. It is important that students understand the need to complete their task thoroughly and thoughtfully, as their group success depends upon it!
Now, send all the numbered students to meet with their group and complete their task:
SUMMARY OF THE TASKS:
- In Task 1, students are asked to expand (x+y)^4, starting with (x+y)^2 and working their way up. This task usually takes the longest for groups to complete, and requires attention to detail. In the end, groups are asked to list the co-efficients of the terms they get.
- In Task 2, students are asked to list the sample space for 4 tossed coins. The task is not difficult, but requires attention to detail in making sure all possibilities are provided. Groups are then asked to list number of ways to get 0 heads, 1 head, 2 heads, etc., in the 4 coins. Note, groups often give probabilities here….we want the COUNTS!
- In Task 3, students complete a number of rows in Pascal’s Triangle. The task in not tricky, but requires attention to detail in filling out the small boxes. The group is then asked to list the numbers in row 4 of the triangle.
- In Task 4, students are asked to compute a number of combinations by formula. I usually try to have 4-function calculators at the ready for this group, and want them to really focus on the formulas. In the end, the group is asked to list the combinations of 4 items taken 0, 1, 2 3 and 4 at a time.
The tasks often take about 20-30 minutes for groups to complete and check. Bringing groups back together and having them share their findings with their teammmates often takes another 20-30 minutes, so this may need to be done over 2 days.
 The big reveal occurs as groups begin to realize that all 4 tasks have the same “answers”:
The big reveal occurs as groups begin to realize that all 4 tasks have the same “answers”:
1-4-6-4-1
We’re now ready to start exploring the amazing connections between 4 ideas (binomials, coins, Pascal’s Triangle, combinations) which seemed quite different math-wise, but have some strong connections. Now the ideas come fast and furious as we explore the connections. Page 5 of the packet provides some guiding questions, but don’t feel tied to the linearity of my questions.
Let’s think about (x+y)^5…..
- How many terms will it have? 6
- How will the powers of x and y behave?
- How can we find the coefficients? Pascal’s Traingle!
- How else can we find the coefficients? Combinations!
How about coin flipping:
- If we flipped 6 coins, how many items would be in the sample space? 2^6
- How many of these possibilities will have all heads? 1
- How can we find out the number of ways to get exactly 2 heads? Pascal’s Triangle
Eventually, this will become the basis for “assembling” the Binomial Theorem. You’ll be surprised at how much of it your students will be able to piece together after this activity. Your job is to just help out with some symbols and some common language.







