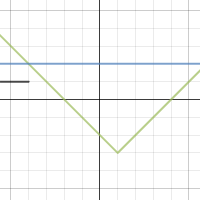
In a recent tour of my midde school, I observed a 6th grade teacher working with a class to use compasses. Their goal: to make a snowman with segments of different, but given radii, 3cm, 2cm and 1cm. Eventually, this will lead to students having their first experience with circumference, and that sneaky number pi. But why tie students to fixed radii values? And just what are the “perfect” measurements for a snowman? Here are some lesson ideas for letting students explore their own snowmen, using technology, then taking it a step further by considering how much snow our snowmen will need.
Snowmen may come in all different sizes, with different accessories. But it is pretty well established that the traditional snowman is made of 3 body segments. Snowmen with anything other than 3 segments are blasphemous.

WHAT ARE THE PERFECT SNOWMAN DIMENSIONS?
Clicking the image to the right will take you to an interactive graph I made using the Desmos calculator. You can manipulate the diameter of each snowman segment by pulling the sliders provided, but the height of the snowman is fixed at 6 feet. Like your snowman with equal segments? Knock yourself out. Are you more of a bottom-heavy snowman connoisseur? There’s room on the bus for you , too.
Once you are convinved that you have built the world’s best snowman, please share your slider settings here. I’d like to feature them in a later blog post.
INVESTIGATING YOUR SNOWMAN
For a classroom discussion, have students print out their snowman images (Desmos has a snazzy print feature), and compare their snowmen in groups. Whose snowman would need the most snow to build? Whose would need the least? Or, if all of the snowmen are 6 feet tall, then will they use the same amount of snow?
This is a great time to talk about volume, and introduce the formula for the volume of a sphere. And, since each student has their own product, have them find the volume of each snowman segment, then add them to get their required snow total.
HOW MUCH SNOW DO WE NEED?
If it snows 5″ overnight, will we have enough snow on the ground to build our snowman? For this next stage, we can have students compare the volume of snow needed for their snowman with the volume of snow on the ground. For example, if your yard is 10 feet long and 10 feet wide, will 5 inches of ground snow be enough to build our snowman?
BUT, we pack snow while we build snowmen. How much less is the snow volume in a snowman vs its volume when it is on the ground? 2 times less volume? 5 times less? 10 times less? I really have no idea. Next time I have a few inches of snow on the ground, it will be experiment time. With a class, perhaps debate the correct number and use it for calculations.

To help with calculations, and checking student work, I have created this handy Snowman Calculator on Excel. You can input your a and b values from the Desmos document, along with the dimensions of a yard or rectangular area. The volume of your snowman, along with needed snowfalls, are then given.
Think warm! And then we will start working on sandcastles.


 Next, provide each student (or pairs) with a few potential input and outputs, writing them on a 3×5 card. 3 or 4 of each will suffice, and try to give a variety of positives and negatives, along with a fraction and/or decimal. Some samples are here.
Next, provide each student (or pairs) with a few potential input and outputs, writing them on a 3×5 card. 3 or 4 of each will suffice, and try to give a variety of positives and negatives, along with a fraction and/or decimal. Some samples are here.