Tag: AP Statistics

Categories
Uncategorized

Thoughts on Calc-Speak

With the inclusion of Desmos as a tool on the digital AP Statistics exam, I have noticed (and responded to) the many questions teachers have about showing work when Desmos is used:

“Do we know anything yet about what Desmos calculator notation will be allowed on the AP Stats exam, similar to the way normalcdf TI notation was allowed?” – via reddit

The short answer here is no…and we won’t know until rubrics for the 2026 exam are released next fall. And while I have some suspicions about how “Desmos speak” could be handled, my first piece of advice is to take a wider view of statistical communication.

I have been involved with the AP Statistics reading since 2012 – as reader, table leader, and now as a table leader working on a rubric team. In the past, labeled calculator speak has been been accepted to earn credit for components of problems – usually calculations of probabilities from normal and binomial distributions – but such labeling demonstrates a low bar for statistical communication. A comment from Corey Andreasen on the AP Stats Facebook group is an exellent summary of this:

To elaborate a bit, calculator syntax was never required, merely tolerated (if labeled) as it does minimally address the necessary components: Identifying the distribution (the word “normal” or a picture of a normal model should appear – normcdf is close enough), parameters (labeled calc syntax does identify mean and sd, but so does a labeled diagram or just listing them), boundary and direction (a shaded and labeled diagram or a proper probability statement does this, but the lower and upper bounds in the calc notation suffice, if labeled). It is better to get students to communicate properly using statistical notation.

PRO-TIP: Encourage students to use standard notation at all times. Place your bar for communication on in-class assessments higher than the AP rubrics.

For example, part a of question 6 from the 2023 exam asks students to find a probability from a normal distribution. The rubric lists 3 components to be met in order to earn full credit. This rubric is typical of similar problems in previous years.

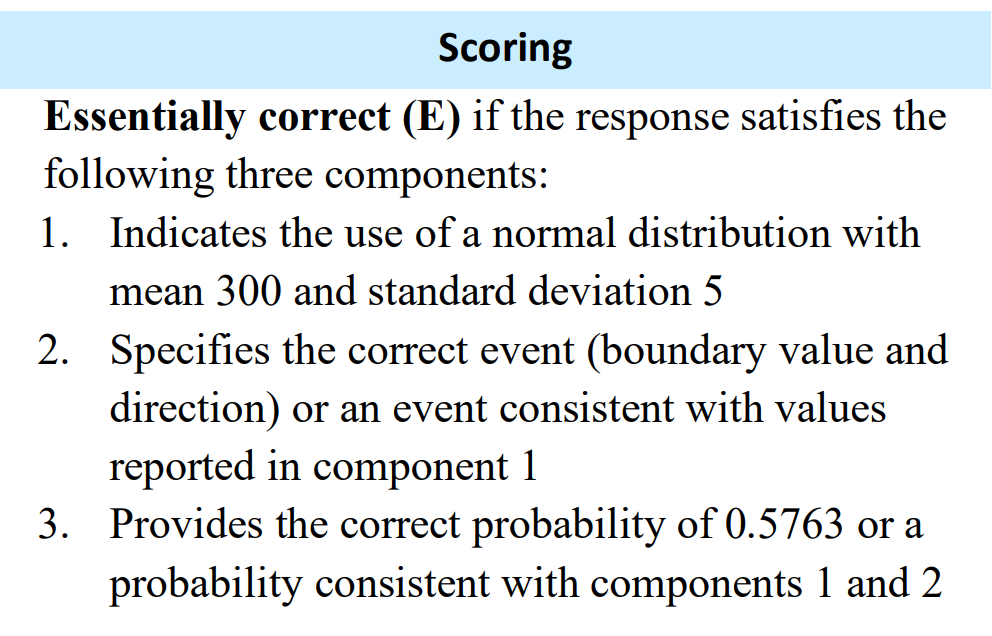
Components 1 and 2 can be met by using standard notation.

On my class assessments, not only do I require students to meet all 3 components, I also require a labeled sketch of the normal distribution and z-score computation. I insist upon the z-score as this will be an important statistic to understand as we start to study inference and compute test statistics.

SO, WHAT ABOUT DESMOS?

The acceptance of calc-speak as evidence for components is listed under the “Notes” section of the rubric.

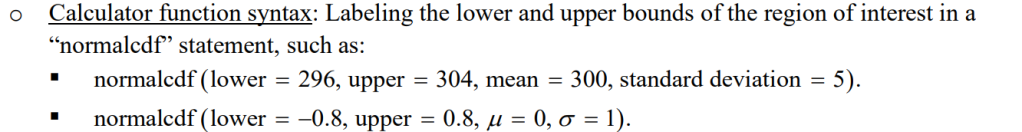
The notes are developed by the chief reader prior to the AP reading, and notes may be added as sample papers are reviewed in the days leading up to the exam reading. So, any scoring notes involving Desmos would likely come from observations of student work. Here is my suggestion about how Desmos language could be incorporated into an existing rubric:

To receive full credit, students would then need to provide an inequality and a correct answer, which is provided on the calculator screen.

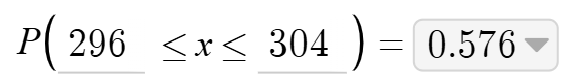
In summary – calc speak…it’s acceptable. But it’s also a great time to take inventory of expectations and move beyond simply acceptable.

Categories
Statistics

Power and Virtual Coins

This activity was inspired by the article “Innocent Until Proven Guilty”, by Catherine Case and Doug Whitaker. NCTM Mathematics Teacher, Volume 109, Issue 9 (May 2016)

Around February each year, the AP Statistics message boards come alive with new and veteran AP Statistics teachers seeking ideas to help students understand the concept of statistical power. While Power is a “minor league” topic in the AP Stats curriculum, a robust discussion of the concept can help tie together the logic of statistical inference: P-values, error and sampling variability. I’ve developed a few activities to try to bring Power to life (see here and here). And while each was satisfying in their own way, none of them really met one of my overarching classroom goals – to have students identify and express a new idea with their groups before I provide clarification. This year’s activity worked nicely as it allowed students to experience statistical power and generate meaningful conversation. Download the student version below, then read to learn how it works.

is-your-coin-fair-powerDownload

In this activity students will investigate the “fairness” of 3 virtual coins through a Desmos graph, using 3 different sample sizes to compile evidence. For each sample, students use their graphing calculator to compute a P-value and then reach a statistical conclusion. For coin A, I led students through the steps for n=10 and encouraged them to work through the next two sample sizes using their group-mates as a support system.

As students completed all three columns for coin A, I asked them to make a final decision regarding the fairness of coin A – is there convincing evidence that coin A is unfair? Students discussed findings with their groups and thoughts about how each column provided convincing evidence. Here is what the class-wide vote and conversation revealed:

  • Of my 42 total students (2 classes), only 1 student concluded that coin A was unfair.
  • All groups agreed that the larger sample size (n=100) was more useful in reaching a decision about the coin.

Spoiler alert: coin A is unfair! If you take a peek under the Desmos hood, you will find that coin A is “programmed” as 48% heads, 52% tails. I didn’t reveal the true proportion until the end, but we are off to a good start here: small differences between the null and “truth” are less likely to be detected.

Groups then tackled coin B with little assistance from me. Working through each column, then the follow-up conversation and decision, took about 5 minutes. This time about 60% of the students concluded that coin B was unfair.

Finally, coin C. Many students quickly concluded that coin C was unfair (it is!) but worked through each of the columns and sample sizes. In the end, there was class-wide agreement that coin C is an unfair coin.

At this point I revealed the truth about each coin:

  • Coin A: 45% heads
  • Coin B: 40% heads
  • Coin C: 25% heads

So, what do our finding show us about hypothesis testing and decision-making as a whole? I was thrilled when one of my students who does not volunteer often raised his hand to offer the following: “If there is a big difference between the null and the truth, it’s easier to reject the null.”

Yes! That’s a big part of power. What else?

Larger sample sizes are more likely to detect a difference when one exists.

Yes! And now we have a nice framework for power. From here I shared a working definition of power and included thoughts on alpha, which are not part of this activity now but could be in a later version.

EmPower your students to develop statistical ideas!

Categories
Statistics

Statistics Arts and Crafts

The Chi-Squared chapter in AP Statistics provides a welcome diversion from the means and proportions tests which dominate hypothesis test conversations. After a few tweets last week about a clay die activity I use, there were many requests for this post – and I don’t like to disappoint my stats friends! I first heard of this activity from Beth Benzing, who is part of our local PASTA (Philly Area Stats Teachers) group, and who shares her many professional development sessions on her school website. I’ve added a few wrinkles, but the concept is all Beth’s.

ACTIVITY SUMMARY: students make their own clay dice, then roll their dice to assess the “fairness” of the die. The chi-squared statistic is introduced and used to assess fairness.

clayYou’ll need to go out to your local arts and crafts store and buy a tub of air-dry clay. The day before this activity, my students took their two-sample hypothesis tests.  As they completed the test, I gave each a hunk of clay and instructions to make a die – reminding them that opposite sides of a die sum to 7. Completed dice are placed on index cards with the students names and left to dry. Overnight is sufficient drying time for nice, solid dice, and the die farm was shared in a tweet, which led to some stats jealousy:

The next day, students were handed this Clay Dice worksheet to record data in our die rolling experiment.

In part 1, students rolled their die 60 times (ideal for computing expected counts), recorded their rolls and computed the chi-squared statistic by hand / formula. This was our first experience with this new statistic, and it was easy to see how larger deviations from the expected cause this statistic to grow, and also the property that chi-squared must always be postivie (or, in rare instances, zero).

Students then contributed their chi-squared statistic to a class graph. I keep bingo daubers around my classroom to make these quick graphs. After all students shared their point, I asked students to think about how much evidence would cause one to think a die was NOT fair – just how big does that chi-squared number need to be? I was thrilled that students volunteered numbers like 11,12,13….they have generated a “feel” for significance. With 5 degrees of freedom, the critical value is 11.07, which I did not share on the graph here until afterwards.

FullSizeRender

In part 2, I wanted students to experience the same statistic through a truly “random” die. Using the RandInt feature on our calculators, students generated 60 random rolls, computed the chi-squared statistic, and shared their findings on a new dotplot.  The results were striking:

FullSizeRender - 3

In stats, variability is everywhere, and activities don’t often provide the results we hope will occur. This is one of those rare occasions where things fell nicely into place. None of the RandInt dice exceeded the critical value, and we had a number of clay dice which clearly need to go back to the die factory.